
Table of Contents
Velocity Measurement By Pitot Static Tube in Subsonic And Supersonic Regime
Do you know how the velocity of an aircraft is measured in a fluid using a Pitot-Static Tube? On road vehicles such as buses, motorcycles, and cars, we have a mechanism consisting of magnetic coils that measure the velocity of the vehicle based on the number of wheel rotations.
Aircraft, however, lack a speedometer mechanism that relies on a road. Instead, fluid pressure is utilized to measure the velocity of the aircraft. In other words, a Pitot-Static tube is installed on the aircraft body to measure its velocity.
Related: Complete Wind Tunnel Technique Notes for PTU & PEC Aero Students
PITOT-STATIC TUBE SYSTEM
The Pitot-Static Tube is an instrument used to measure fluid flow velocity. It is comprised of two components: the Pitot tube and the Prandtl tube. The Pitot tube features a total hole, as depicted in the image below, while the Prandtl tube is equipped with static holes located around the tube’s periphery.

The Pitot-Static Tube combines the design of the Pitot tube and the Prandtl tube, making it effective for measuring fluid flow in high Reynolds number conditions and at different altitudes and angles of attack. The inclusion of static holes allows for the measurement of accurate velocity by capturing the static pressure of the surrounding atmosphere. This makes the Pitot-Static Tube suitable for measuring the velocity of various bodies such as aircraft, ships, and rocket sleds.
Stagnation Pressure= Static Pressure + Dynamic Pressure
PITOT STATIC TUBE AIR FLOW MEASUREMENT IN SUBSONIC AND SUPERSONIC FLOW REGIME
Following is the subsonic to supersonic flow regime information:-
-
SUBSONIC FLOW REGIME(UP TO MACH 0.3)
For free stream velocities up to Mach 0.3 (103 m/s), where the flow is considered incompressible, we can utilize Bernoulli’s equation to measure velocity. Bernoulli’s equation describes the relationship between velocity and pressure in streamlined flow.
-
SUBSONIC COMPRESSIBLE FLOW REGIME MACH 0.3< 1
For velocities exceeding Mach 0.3, the flow is considered compressible, and the density of the flow varies from point to point. When the flow encounters the nose of the Pitot-Static tube, the air undergoes compression. In this scenario, we assume that the flow is compressed and decelerated isentropically from its free stream state.
-
SUPERSONIC FLOW REGIME MACH 1<M<5
A new phenomenon occurs for flows exceeding Mach 1, where shock waves are formed upstream of the Pitot-Static tube’s nose. These shock waves decelerate the flow in a non-isentropic manner, transitioning it from supersonic to subsonic conditions. This process brings the velocity to zero Isentropically near the stagnation point. The diagram below illustrates this phenomenon.
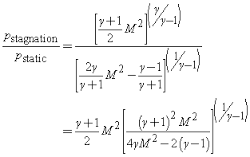
In the supersonic regime, the flow velocity is an implicit function of the Pitot tube pressure. To measure velocity in this regime, the Rayleigh formula is employed.
Where;
- P02 =Pressure of free stream at the stagnation point.
- P1 =Pressure of free stream in front of shock waves(static pressure)
- M1= Free stream Mach number before shock waves
- M2= Free stream Mach number after the shock waves
- x= (Gamma ) Ratio of specific heat at constant pressure to specific heat at constant volume

